Moment-Curvature Analysis

In this example a moment-curvature analysis is performed for steel and concrete sections.

import veux
import numpy as np

from xsection.analysis import SectionInteraction

import matplotlib.pyplot as plt
# plt.style.use("veux-web")

Steel

import xara.units.fks as units
from xara.units.fks import kip, ksi

from xsection.library import from_aisc
shape = from_aisc("W14x426", units=units)
veux.render(shape.model)

For the material model, the \(J_2\) plasticity formulation is used.

steel = {
        "type": "J2",
        "nu": 0.3,
        "E":  29000*ksi,
        "Fy":    50*ksi,
        "Hiso": 0.003*29e3*ksi,
        "Fs": 0, "Fo": 0, "Hsat": 16
}

Ny = shape.area*steel["Fy"]

axial = np.linspace(-Ny, Ny, 10)

si = SectionInteraction(("ShearFiber", shape, steel), axial=axial)

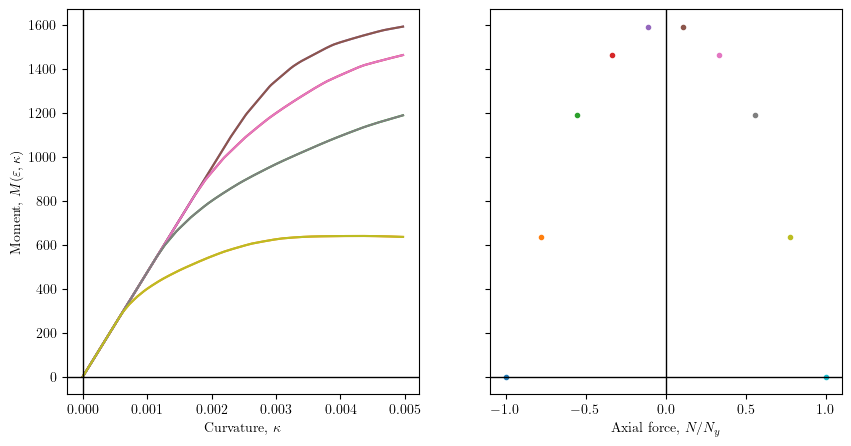
fig, ax = plt.subplots(1,2, figsize=(10, 5), sharey=True)

for N, M, k in si.moment_curvature():
    ax[0].plot(k, M, '-') #, label=f"{N/kip:.0f} kip")
    ax[1].plot([N/Ny], [M[-1]], '.')


ax[0].axvline(0, color="k", lw=1)
ax[0].axhline(0, color="k", lw=1)
ax[1].axvline(0, color="k", lw=1)
ax[1].axhline(0, color="k", lw=1)
ax[0].set_xlabel("Curvature, $\\kappa$")
ax[0].set_ylabel("Moment, $M(\\varepsilon, \\kappa)$")
ax[1].set_xlabel("Axial force, $N/N_y$");

   FAILURE :: Iter:    20, Norm:     14.7574, Norm deltaX: 2.25907e-05
   FAILURE :: Iter:    20, Norm:     14.7574, Norm deltaX: 2.25907e-05

Concrete

Geometry

from xsection.library import Rectangle, Circle
from xsection import CompositeSection

h = 24
b = 15
d = 7/8
r = 0 #d/2

c = 1.5

bar = Circle(d/2, z=2, mesh_scale=1/2, divisions=4, name="rebar")

shape = CompositeSection([
            Rectangle(    b, h,     z=0, name="cover"),
            Rectangle(b-2*c, h-2*c, z=1, name="core"),
            *bar.linspace([-b/2+c+r, -h/2+c+r], [ b/2-c-r,-h/2+c+r], 3), # Top bars
            *bar.linspace([-b/2+c+r,        0], [ b/2-c-r,       0], 2), # Center bars
            *bar.linspace([-b/2+c+r,  h/2-c-r], [ b/2-c-r, h/2-c-r], 3)  # Bottom bars
        ])


print(shape.elastic.summary())

artist = veux.create_artist(shape.model) #veux.model.FiberModel(shape.create_fibers()))
# artist.draw_samples()
artist.draw_outlines()
artist.draw_surfaces()
artist

  Iy : 1.728e+04
  Iz : 6750
   A : 360
  Ay : 302.1
  Az : 300.9
   J : 1.669e+04
 Iyz : -4.157e-13

Analysis

from xara.units.iks import kip, ksi

mat = [
    { # Confined
        "name": "core",
        "type": "Concrete01",
        "Fc":   6*ksi,
        "ec0":  0.004,
        "Fcu":  5*ksi,
        "ecu":  0.014,
    },
    { # Unconfined
        "name": "cover",
        "type": "Concrete01",
        "Fc":  -5*ksi,
        "ec0": -0.002,
        "Fcu":  0,
        "ecu": -0.006,
    },
    {
        "name": "rebar",
        "type": "Steel01",
        "E":   30e3*ksi,
        "Fy":    60*ksi,
        "b":   0.01
    }
]

axial = np.linspace(-1200*kip, 250*kip, 15)

si = SectionInteraction(("Fiber", shape, mat), axial=axial)

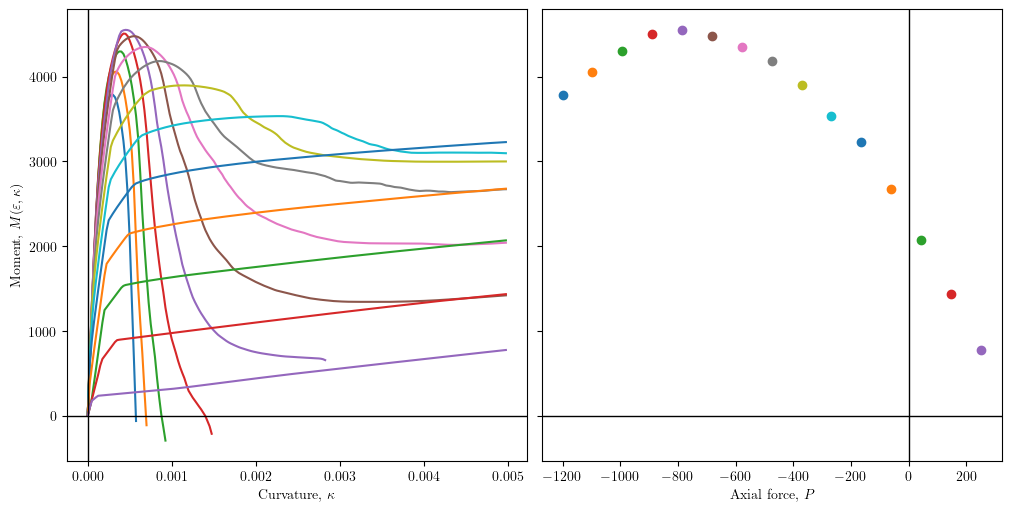
fig, ax = plt.subplots(1,2, sharey=True, constrained_layout=True, figsize=(10, 5))
mmax = []

for n, m, k in si.moment_curvature():
    ax[0].plot(k, m, '-')

    # ax[1].plot([n]*len(m), m, '-', lw=0.3, markersize=0.5)
    ax[1].plot([n], [max(m)], 'o')

ax[0].axvline(0, color="k", lw=1)
ax[0].axhline(0, color="k", lw=1)
ax[1].axvline(0, color="k", lw=1)
ax[1].axhline(0, color="k", lw=1)
ax[0].set_xlabel("Curvature, $\\kappa$")
ax[0].set_ylabel("Moment, $M(\\varepsilon, \\kappa)$")
ax[1].set_xlabel("Axial force, $P$");

   FAILURE :: Iter:    20, Norm:      173.55, Norm deltaX:  0.00061013
   FAILURE :: Iter:    20, Norm:     152.911, Norm deltaX: 0.000600928
   FAILURE :: Iter:    20, Norm:     24.0361, Norm deltaX: 0.000190103
   FAILURE :: Iter:    20, Norm:     13.3266, Norm deltaX: 4.13907e-05
   FAILURE :: Iter:    20, Norm:     4.70975, Norm deltaX: 0.000169825

Text(0.5, 0, 'Axial force, $P$')

from xsection.library import Circle, Equigon
from xara_units.iks import inch, foot 

d = 11/8*inch
ds = 4/8*inch # diameter of the shear spiral
cover = (3 + 1/8)*inch
core_radius = 5/2*foot - cover - ds - d/2
nr = 12

octagon  = Equigon(5*foot/2, z=0,
                    name="cover", divisions=8)

interior = Equigon(core_radius, z=1,
                    name="core", divisions=nr)

bar = Circle(d/2, z=2, mesh_scale=1/2, divisions=4, name="rebar")

xr = ((5*foot/2) - cover - ds - d/2, 0)


shape = CompositeSection([
            octagon,
            interior,
            *bar.linspace(xr, xr, nr, endpoint=False, center=(0,0))
        ])

print(shape.elastic.summary())

artist = veux.create_artist(shape.model) #veux.model.FiberModel(shape.create_fibers()))
# artist.draw_samples()
artist.draw_outlines()
artist.draw_surfaces()
artist

  Iy : 7.094e+05
  Iz : 7.094e+05
   A : 2982
  Ay : 2553
  Az : 2553
   J : 1.396e+06
 Iyz : 2.717e-11